Estimates with a value, 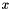 , and a variance,
, and a variance, 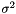 .
More...
.
More...
#include <Estimate.h>
|
|
typedef T | val_type |
| |
|
typedef U | var_type |
| |
|
|
| Estimate (T _val=0, U _var=0) |
| | Construct from a value, 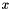 , and its variance, , and its variance,  . .
|
| |
|
template<typename V , typename W > |
| | Estimate (const Estimate< V, W > &d) |
| | Construct from another Estimate.
|
| |
|
template<typename V , typename W > |
| | Estimate (const MeanEstimate< V, W > &m) |
| | Construct from MeanEstimate.
|
| |
|
template<typename V , typename W > |
| | Estimate (const MeanRadian< V, W > &m) |
| | Construct from MeanRadian.
|
| |
|
const Estimate & | operator= (const Estimate &d) |
| | Assignment operator.
|
| |
|
void | set_value (const T &t) |
| | Set the value.
|
| |
|
T | get_value () const |
| | Get the value.
|
| |
|
void | set_variance (const U &u) |
| | Set the variance.
|
| |
|
U | get_variance () const |
| | Get the variance.
|
| |
|
void | set_error (const U &u) |
| | Set the error.
|
| |
|
U | get_error () const |
| | Get the error.
|
| |
|
T & | operator[] (unsigned) |
| | Array access to value.
|
| |
|
T | operator[] (unsigned) const |
| | Array access to value.
|
| |
|
const Estimate & | operator+= (const Estimate &d) |
| | Addition operator.
|
| |
|
const Estimate & | operator-= (const Estimate &d) |
| | Subtraction operator.
|
| |
| const Estimate & | operator*= (const Estimate &d) |
| | Multiplication operator. More...
|
| |
|
const Estimate & | operator/= (const Estimate &d) |
| | Division operator.
|
| |
|
bool | operator== (const Estimate &d) const |
| | Equality operator.
|
| |
|
bool | operator!= (const Estimate &d) const |
| | Inequality operator.
|
| |
|
bool | operator< (const Estimate &d) const |
| | Comparison operator.
|
| |
|
bool | operator> (const Estimate &d) const |
| | Comparison operator.
|
| |
| const Estimate | inverse () const |
| | Inversion operator. More...
|
| |
|
|
T | val |
| | The value, 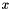 . .
|
| |
|
U | var |
| | The variance of the value,  . .
|
| |
template<typename T, typename U = T>
class Estimate< T, U >
Estimates with a value, 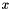 , and a variance,
, and a variance, 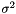 .
.
Where 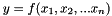 , then
, then 
See http://mathworld.wolfram.com/ErrorPropagation.html
◆ inverse()
template<typename T, typename U = T>
◆ operator*=()
template<typename T, typename U = T>
The documentation for this class was generated from the following file:
 PSRCHIVE
PSRCHIVE
 PSRCHIVE
PSRCHIVE
 Home
Home